
It can be a whole number, a fraction, or even an irrational number. The common ratio can be positive or negative. If you multiply any term by this value, you end up with the value of the next term.įor an existing Geometric Sequence, the common ratio can be calculated by dividing any term by its preceding term:Įvery Geometric Sequence has a common ratio between consecutive terms. Since all of the terms in a Geometric Sequence must be the same multiple of the term that precedes them (3 times the previous term in the example above), this factor is given a formal name (the common ratio) and is often referred to using the variable (for Ratio). So represents the value of the first term in the sequence (5 in the example above), and represents the value of the fifth term in the sequence (405 in the example above). The one is a “subscript” (value written slightly below the line of text), and indicates the position of the term within the sequence. This notation is read as “A sub one” and means: the 1st value in the sequence or progression represented by “a”. To refer to the first term of a sequence in a generic way that applies to any sequence, mathematicians use the notation In the example above, 5 is the first term (also called the starting term) of the sequence or progression. Now, continue multiplying each product by the common ratio (3 in my example) and writing the result down… over, and over, and over:īy following this process, you have created a “Geometric Sequence”, a sequence of numbers in which the ratio of every two successive terms is the same. Now multiply the first number by the common ratio, then write their product down to the right of the first number: Now pick a second number, any number (I’ll choose 3), which we will call the common ratio. Pick a number, any number, and write it down.
Nth term equation maker how to#
So, let’s investigate how to create a geometric sequence (also known as a geometric progression). This post uses the term “sequence”… but if you live in a place that tends to use the word “progression” instead, it means exactly the same thing. A “geometric sequence” is the same thing as a “geometric progression”. There are of course many more ways to construct sequences but the ones mentioned here are some of the most common.The terms “sequence” and “progression” are interchangeable.
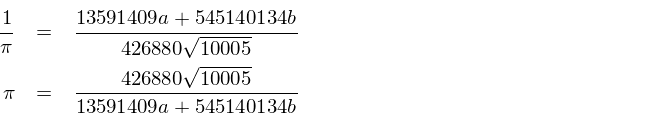
In addition to what has been mentioned already the tool can also recognize the sequence of prime numbers and the Fibonacci sequence. The reason the tool does not always find a polynomial has to do with technical limitations that makes the numeric precision not good enough for polynomials of higher degrees. This is something to think about when using the tool on this page. For this the polynomial degree would have to be two (preferable three or more) degrees lower than the number of known numbers in the sequence. If n numbers are known it is always possible to find a polynomial of degree n - 1 that match all the numbers, but this does not necessarily describe any true pattern of the sequence. Note that as long as you have a finite sequence of numbers it is always possible to find a polynomial that can describe it. For fourth degree polynomials we would have to look at yet another level of differences. To solve a third degree polynomial the difference between the differences between the differences need to be constant. Sometimes it can be necessary to use polynomials of higher degree than two but the method is essentially the same.

To establish the polynomial we note that the formula will have the following form. This tells us that it is possible to describe the sequence as a second degree polynomial but it does not give us any information about how. If we look at the difference between the five initial numbers we find that they are 3 5 7 9 and, as you can see, the differences between these numbers are 2. 2 5 10 17 26… is an example of such a sequence. If it turns out that the difference between the differences is constant it means that the sequence can be described using a second degree polynomial. If neither quotient nor difference is constant it might be a good idea to look at the difference between the differences. This sequence can be described using the exponential formula a n = 2 n. 2 4 8 16… is an example of a geometric progression that starts with 2 and is doubled for each position in the sequence. In a geometric progression the quotient between one number and the next is always the same. This sequence can be described using the linear formula a n = 3 n − 2.

1 4 7 10 13… is an example of an arithmetic progression that starts with 1 and increases by 3 for each position in the sequence. In an arithmetic progression the difference between one number and the next is always the same.


 0 kommentar(er)
0 kommentar(er)
